Значок перпендикулярности в ворде

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).

В Word можно вставлять математические символы в уравнения и текст.

На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.

В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.

Щелкните стрелку рядом с названием набора символов, а затем выберите набор символов, который вы хотите отобразить.

Щелкните нужный символ.

Доступные наборы символов

В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.

Основные математические символы

Часто используемые математические символы, такие как > и

Вопрос решен и закрыт.

Лучший ответ

Енот 8 (337417) 6 26 633 6 лет

Ответы

FighteR (30) 7 (88378) 7 26 967 6 лет

ПРОЖЕКТОР 6 (9106) 3 13 43 6 лет

радует, что у некоторых очень не плохо развито ассоциативное мышление! Причем морфологически безупречное .))

Ylarya 6 (6586) 2 4 15 6 лет

Vadinho 6 (16535) 3 41 85 6 лет

Похожие вопросы

Это лого фирмы Ямаха. 3 скрещённых камертона (небольшой портативный прибор, точно и ясно издающий звук определённой высоты со слабыми гармоническими призвуками.)
Скорее всего на уроках музыки вам это рассказывали.

Для обозначения перпендикулярности имеется общепринятый символ: ⊥ <displaystyle perp > , предложенный в 1634 году французским математиком Пьером Эригоном. Например, перпендикулярность прямых m <displaystyle m> и n <displaystyle n> записывают как m ⊥ n <displaystyle mperp n> .

Содержание

На плоскости [ править | править код ]

Перпендикулярные прямые на плоскости [ править | править код ]

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

Про прямую m <displaystyle m> перпендикулярную к прямой ℓ <displaystyle ell > проведённую через точку P <displaystyle P> вне прямой ℓ <displaystyle ell > , говорят, что m <displaystyle m> есть перпендикуляр опущенный из P <displaystyle P> на ℓ <displaystyle ell > . Если же точка P <displaystyle P> лежит на прямой ℓ <displaystyle ell > , то говорят, что m <displaystyle m> есть перпендикуляр к восстановленный из P <displaystyle P> к ℓ <displaystyle ell > (устаревший термин восставленный [1] ).

В координатах [ править | править код ]

В аналитическом выражении прямые, заданные линейными функциями

y = a ⋅ x + b <displaystyle y=acdot x+b>

y = k ⋅ x + m <displaystyle y=kcdot x+m>

будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты

a ⋅ k = − 1. <displaystyle acdot k=-1.>

Построение перпендикуляра [ править | править код ]

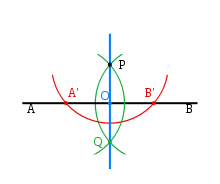
Шаг 1: С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.

Шаг 2: Не меняя радиуса, построим две полуокружности с центром в точках A и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.

Координаты точки основания перпендикуляра к прямой [ править | править код ]

Пусть прямая задаётся точками A ( x a , y a ) <displaystyle A(x_,y_)> и B ( x b , y b ) <displaystyle B(x_,y_)> . На прямую опускается перпендикуляр из точки P ( x p , y p ) <displaystyle P(x_

,y_

)> . Тогда основание перпендикуляра O ( x o , y o ) <displaystyle O(x_,y_)> можно найти следующим образом.

Если x a = x b <displaystyle x_=x_> (вертикаль), то x o = x a <displaystyle x_=x_> и y o = y p <displaystyle y_=y_

> . Если y a = y b <displaystyle y_=y_> (горизонталь), то x o = x p <displaystyle x_=x_

> и y o = y a <displaystyle y_=y_> .

Во всех остальных случаях:

x o = x a ⋅ ( y b − y a ) 2 + x p ⋅ ( x b − x a ) 2 + ( x b − x a ) ⋅ ( y b − y a ) ⋅ ( y p − y a ) ( y b − y a ) 2 + ( x b − x a ) 2 <displaystyle x_=<frac -y_)^<2>+x_

cdot (x_-x_)^<2>+(x_-x_)cdot (y_-y_)cdot (y_

-y_)><(y_-y_)^<2>+(x_-x_)^<2>>>> ; y o = ( x b − x a ) ⋅ ( x p − x o ) ( y b − y a ) + y p <displaystyle y_=<frac <(x_-x_)cdot (x_

-x_)><(y_-y_)>>+y_

> .

В трёхмерном пространстве [ править | править код ]

Перпендикулярные прямые [ править | править код ]

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.

Перпендикулярность прямой к плоскости [ править | править код ]

Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.

Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярные плоскости [ править | править код ]

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

• Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
• Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
• Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
• Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения [2] .

В многомерных пространствах [ править | править код ]

Перпендикулярность плоскостей в 4-мерном пространстве [ править | править код ]

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно ( 4 2 ) = 6 <displaystyle < binom <4><2>>=6> : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости [ править | править код ]

Пусть задано n-мерное евклидово пространство R n <displaystyle mathbb ^> (n>2) и ассоциированное с ним векторное пространство W n <displaystyle W^> , а прямая l с направляющим векторным пространством L 1 <displaystyle L^<1>> и гиперплоскость Π k <displaystyle Pi _> с направляющим векторным пространством L k <displaystyle L^> (где L 1 ⊂ W n <displaystyle L_<1>subset W^> , L k ⊂ W n , k n <displaystyle L^subset W^, k ) принадлежат пространству R n <displaystyle mathbb ^> .

Прямая l называется перпендикулярной гиперплоскости Π k <displaystyle Pi _> , если подпространство L 1 <displaystyle L_<1>> ортогонально подпространству L k <displaystyle L^> , то есть ( ∀ a → ∈ L 1 ) ( ∀ b → ∈ L k ) a → b → = 0 <displaystyle (forall <vec >in L_<1>) (forall <vec >in L_) <vec ><vec >=0>